Cyklotronen

Den magnetiske kraft på en ladet partikel (med ladning q), der bevæger sig med hastigheden

Den magnetiske kraft står vinkelret på både hastigheden og magnetfeltet .

Den effekt, som den magnetiske kraft udfører, er givet ved

Så den magnetiske kraft vil ikke ændre den ladede partikels kinetiske energi,

den ændrer kun hastighedens retning.

Hvis hastigheden har samme retning som magnetfeltet,

så virker der ikke nogen magnetisk kraft på den ladede partikel.

Ser vi på en ladet partikel, der bevæger sig i et homogent magnetfelt ,

kan vi opløse hastigheden i  ,

hvor er hastighedskomposanten af parallelt med B, som ikke ændrer sig.

Partiklen bevæger sig langs , mens den udfører en cirkelbevægelse i den plan, der dannes af og .

Den resulterende banekurve bliver en spiral, hvis akse er parallel med ,

Impulsen bliver ,

og vinkelhastigheden for cirkelbevægelsen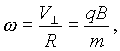

som altså er uafhængig af hastigheden for den ladede partikel!

( er cyklotronfrekvensen)

Det, at cyklotronfrekvensen er konstant førte til en opfindelse kaldet en cyklotron.

Med denne java-applet kan du se nærmere på cyklotronen.

Dette er et ovenfra-billede af det område af cyklotronen, hvor partiklen accelererer.

Klik her for at se et billede af en rigtig cyklotron.

De to hule D-formede objekter (åbne på den lige flade) er lavet af kobberplader.

Disse dees, som de kaldes (dee for d), udgør en del af en elektrisk oscillator,

som lægger en skiftende potentialforskel over gabet imellem dem.

Samtidig befinder de sig i et magnetfelt, hvis retning peger ind i skærmens plan.

Lad os sige, at en proton, der starter fra den blå prik nær cyklotronens centrum,

til at begynde med bevæger sig mod et negativt dee;

Så vil den accelerere mod dette dee og vil bevæge sig ind i det.

Når det først er kommet herind, er det "afskærmet" for elektriske felter af dee'ets kobbervægge.

Magnetfeltet er ikke afskærmet af det (ikke-magnetiske) kobberdee,

så protonen udfører her en cirkelbevægelse.

I det øjeblik protonen (igen) bevæger sig fra den første dee og ud i gabet midt mellem de to dees,

så har den accelererende potentialforskel skiftet fortegn.

Derved står protonen overfor en negativt ladet dee og accelereres igen.

Denne proces fortsætter, således at den cirkulerende proton hele tiden er i takt med omskiftene i dee-potentialet,

indtil protonen spiralerer ud ved randen af dee-systemet.

Frekvensen af den elektriske oscillator skal hele tiden matche cyklotronfrekvensen.

Hvis gabet imellem de to dees er meget lille, er de to frekvenser ens.

Hvad nu, hvis gabet ikke er lille? Så bliver man nødt til at justere frekvensen for den elektriske oscillator.

Indskriv en værdi for frekvensforholdet (oscillatorfrekvens/cyklotronfrekvens) i tekstfeltet.

Klik på den røde prik nær den elektriske oscillator og træk op/ned for at ændre spændingsforskellen.

Klik på Start for at starte animationen,

højreklik for at stoppe, og højreklik igen for at fortsætte.

Den ladede partikels hastighed er repræsenteret ved den gule pil.

Kraften på partiklen er repræsenteret ved den røde pil.

Vy-Vx (hastighederne) for den ladede partikel vises til højre i vinduet.

Klik på Clear for at slette sporet af banekurven.

Klik på Reset for at nulstille værdierne.

For en elektron: Ladning , masse ,

Hvis elektronens energi er 1eV (accelereret under 1V jævnspænding)

og magnetfeltets styrke er 1T (Tesla),

så bliver cyklotronfrekvensen 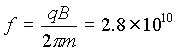Hz. (Det er meget!)

Elektronens hastighed bliver   (Det er hurtigt!)

Hvis hastigheden er vinkelret på magnetfeltet, bliver radius i cirkelbevægelsen

(Det er småt!)

Dersom hastigheden har en lille komposant langs det magnetiske felt (lad os sige 1%),

så vil elektronen bevæge sig langs de magnetiske feltlinier med en hastighed på .

Det er svært at forestille sig elektronens bevægelse under ovenstående betingelser!

Your suggestions are highly appreciated! Please click hwang@phy03.phy.ntnu.edu.tw

Author:Fu-Kwun Hwang, Dept. of physics, National Taiwan Normal University

Last modified:  More physics related java applets